unknown

Aim: Finding and mastering new rational ideas for solving algebraic equations.

Solution

$tema4_EN_files\tema4_EN_MathML_1.jpg$

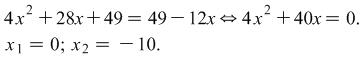
$tema4_EN_files\tema4_EN_MathML_2.jpg$

Solution

$tema4_EN_files\tema4_EN_MathML_4.jpg$ i.e. the number 2 is represented as the sum of 1+1.

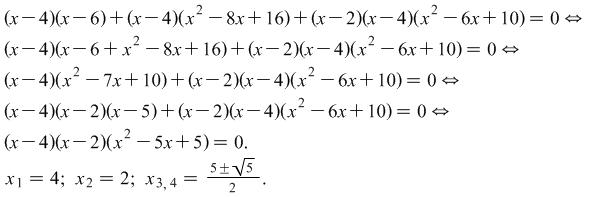
$tema4_EN_files\tema4_EN_MathML_5.jpg$

Solution If we use the standard method - eliminating the denominator $tema4_EN_files\tema4_EN_MathML_7.jpg$ and doing subsequent transformations we get the equation $tema4_EN_files\tema4_EN_MathML_8.jpg$ . We find the divisors of the free term, they are 32 numbers and through direct verification the roots of the equation are found.

The problem can be solved more rationally if the person solving it guesses that here the number 3 is suitable to be represented as 4-1.

Then the given equation can be presented in the form $tema4_EN_files\tema4_EN_MathML_9.jpg$ $tema4_EN_files\tema4_EN_MathML_10.jpg$

The roots of the given equation are $tema4_EN_files\tema4_EN_MathML_11.jpg$

For individual work

Problem 1. Solve the equation $tema4_EN_files\tema4_EN_MathML_12.jpg$ .

Answer $tema4_EN_files\tema4_EN_MathML_13.jpg$ .

Problem 2. Solve the equation $tema4_EN_files\tema4_EN_MathML_14.jpg$ .

Answer $tema4_EN_files\tema4_EN_MathML_15.jpg$ .